LINEAR EQUATIONS

Definition of Linear Equation
Graph of Linear Equation
Linear Equation in one variable
Linear Equation in two variables
Example of Linear Equation in daily life
LINEAR EQUATIONS
In Mathematics, a Linear Equation is an equation of combination of variables, coefficient, and constants in which the highest degree of equation is 1. i.e. An equation that has highest degree of 1 is known as Linear Equation.
There are linear equations in one variable and linear equations in two variables.
The standard form of linear equation in one variable is Ax + B = 0 where, ‘x’ is variable; ‘A’ is coefficient of x; and ‘B’ is constant.
The standard form of linear equation in two variables is Ax + By = C where, ‘x’ is variable; ‘A’ and ‘B’ are coefficients of x and y respectively; and ‘C’ is constant.
Definition: A linear equation is an algebraic equation where each term has an exponent of 1. Therefore we can easily identify equations as linear or non-linear. Non-Linear equations are those where highest power is not 1.
Graph of linear equation: The graph of linear equation always forms a straight line.
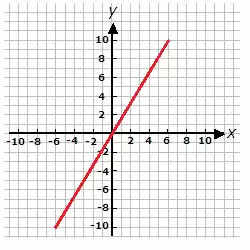
Linear Equations in One Variable:
A linear equation in one variable is an equation in which there is only one variable. It is of the form Ax + B = 0, where A and B are any two real numbers and x is a variable. It has only one solution. It is the easiest way to represent a mathematical statement. The degree of this equation is always equal to 1.
For example, 3x + 7 = 6; 5x + 8 = 0; 2x + 1 = 13
Linear Equations in Two Variables:
A linear equation in two variables is of the form Ax + By + C = 0, in which A, B, C are real numbers and x and y are the two variables, each with a degree of 1.
For example, 6x + 2y + 9 = 0; 4x + 4y = 23; 5x + y = 10
Example of linear equation in daily life:
If your office is 30 miles, and you have reached at 8 am, and you know that the traffic is moving at 60 miles per hour. To know what time you should leave from home, use this equation
Time taken = distance/ rate of travel
t= 30/60 = ½ hour. i.e. To reach the office at 8 a.m., you should leave home at 7: 30 am.
